We should run Wigner's Friend experiments

Quantum Computing comes for Metaphysics

This blog post is about whether free choice and objective reality can coexist - not philosophically, but empirically - and how the tools of quantum computing could help us figure it out.

Quantum computing and the broader field of quantum information is special because it lets you do two things at the same time: (1) build technology that one day could help lots of people and (2) explore the fundamental relationship between reality and information. This combination of applications and foundations makes our field dynamic and rich.

Recently, you may have heard a lot about the applications side. This makes sense: the emerging quantum technology industry wants to tackle practical problems in areas like simulation, optimization, machine learning, and sensing. My own recent publications have focused on how we might get quantum advantage in valuable applications [1] [2] [3] and on what tools can help us get there [4] [5].

But there is more. Better and better quantum technology can drive deeper, more sophisticated experiments that uncover fundamental truths. And it’s timely too! The Nobel Prize in physics from just a few days ago was awarded for just this kind of work. People talk about how scientists today should be more ambitious, so I’m going to lean in and tell you about the most ambitious thing I can think of building.

I’m going to tell you now about some experiments that could dramatically shift our reality: Wigner's Friend experiments.

A Wigner's Friend experiment isn't a single apparatus or setup, but refers to a set of experiments and experimental proposals that are designed to answer a similar question. The first thought experiment of this kind was proposed by Eugene Wigner in 1961, which gives it this name. We’ll focus the discussion here on more modern versions. 

The experiments are certainly ambitious. In the long term, it might involve making a human version of Schroedinger’s cat… but bear with me, because the outcome is incredibly important, and we might be able to make more headway than folks have previously realized.

What might we learn from a Wigner's Friend experiment?

Wigner's Friend is a foundational experiment because it tells us about meta-physics. It not only tells us about how well our current theory, quantum mechanics, corresponds to reality, but it also tells us about how any future theories must behave (that is, if they are going to be consistent with the experimental results that we observe). If Wigner's Friend tells us something weird, which it does, then that weirdness is not contingent but fundamental. What it tells us about reality won’t change if only we had better instruments or had supercharged AI assistants planning our experiments.

In imprecise terms, Wigner's Friend experiments ask whether we can have both free choice and a single objective reality (under reasonable definitions). Surprisingly, if quantum mechanics applies at large scales in ways that most scientists think it does, then we expect the experiment to show that we have to either (1) give up objective reality or (2) give up free choice. A properly implemented Wigner's Friend experiment thus has two outcomes:

1. Everything proceeds as predicted by quantum theory, violating either objective reality or free choice. Take your pick. In my view, objective reality is the one to go and the result would provide the first experimental evidence that different observers can exist in different incompatible realities. This means that the experiment will break reality apart into different, incompatible pieces called Wigner bubbles.

2. We get a result that is not predicted by quantum theory. This means we’ve gained insight into new limitations on quantum mechanics, advancing our understanding in a totally new way. Breaking quantum mechanics would also be deeply impactful. New results could give insights for quantum gravity research, new types of computing, and/or resolve the “interpretation problems” of quantum mechanics.
   ‍

If you are thinking that this talk of objective reality and free choice sounds like an introspective philosophical discussion, then I don’t blame you. However, we are talking about something more here. The magic of Wigner's Friend is that we can take a question about the compatibility of objectivity and free choice and build an experiment, a machine, to physically test the outcome. We can bring the evidence of science and physics to a metaphysical question.

This Document

We proceed in the following steps. First, we introduce more precise definitions for concepts related to objective reality and free choice. Next, we’ll review what the Wigner's Friend experiment is. We’ll focus on a version called the Possibilistic Extended Wigner's Friend Experiment, following the recent work of Hadarra & Cavalcanti. This is a modern variant of Wigner's Friend that has the weakest assumptions and a simple derivation. After that, we’ll show how a contradiction can arise in the experimental outcome. Finally, I’ll raise some questions that could help us make progress on this experiment in the near-term.

What might we learn from Wigner's Friend experiments? (now with more precise definitions)

There are two assumptions about the world that a Wigner's Friend experiment could show are contradictory:

Absoluteness of Observed Events (AOE): An observed event is real and objective. It is not relative to anyone.

You can take this to mean: there is one reality that we all share. We might see different parts of it at different times, but fundamentally there is one reality that is observed. Note that relativity is consistent with this assumption. We may be in different reference frames, but these frames give different perspectives on the same underlying reality. A violation of AOE makes reality subjective in a much stronger way than relativity does. Events that you observe aren’t just observed differently by me: in my reality, they might not happen at all.

Possibilistic Local Agency (PLA): Causes can only have effects within their future light cone.

Relativity tells us that the speed of light is an ultimate speed limit on interactions. Imagine that I am one light year away from you. If I send out some big signal or interaction right now, then the soonest it can interact with you is one year from now. You can be sure that your decisions (and any experiments that you do) within the next year can’t be affected by me. In other words, my action only affects observations that are reachable from me within the speed of light. You could replace the speed of light with some other local limit - say, twice as fast, or 10 times slower - and the underlying Wigner's Friend argument stands.

If you drop the PLA assumption, then you can be affected at any time by anything in any part of the universe. That’s a shaky foundation to build a consistent theory of reality on top of. Without this assumption, one has recourse to say things like: your experiment got that outcome today, not because of an underlying physical law you’ve discovered, but because some arbitrary configuration of matter hundreds of light years away happened to interact with it. Alternatively, you would have to allow for events from the future to influence the past, e.g. the signal that I send from one light year away still takes one light year to get to you but your future receipt of that signal could affect what happens to you today.

Both of these assumptions appear fundamental and uncontroversial. An experiment that gives evidence that we need to drop one of them would be radical. That is what Wigner's Friend experiments can do.

What is the experiment?

The original Wigner's Friend thought experiment was described by Wigner in 1961, and has been refined in several forms and extensions over the years. For this discussion, I’m going to focus on a recent version: the Possibilistic Extended Wigner's Friend Scenario (PEWFS) from Haddara and Cavalcanti. This version has weak assumptions (just the two above of AOE and PLA) and a simple description.

The experiment involves four observers (Alice, Bob, Charlie, and Debbie) and a few components: 

1. Alice has a friend Charlie who is sealed inside an isolated laboratory.
   ‍
2. Bob has a friend Debbie who is sealed inside a different isolated laboratory.
   ‍
3. There is a physical system S that can be broken into two parts S_C and S_D. One part is given to Charlie and the other part is given to Debbie. You can imagine that this is a pair of photons.
   ‍
4. The laboratories that contain Charlie and Debbie need to be far enough apart that the PLA assumptions means that one doesn’t affect the other (after the pieces of the system have been given out), as long as we perform the pieces of the experiment quickly enough.
   ‍
5. Measurements on each S_i give binary outcomes, e.g. 0 or 1. Charlie and Debbie make measurements of their respective part of the system, and they have outcomes labeled as c, d ∈ {0, 1}. For example Charlie and Debbie could measure the polarization of the photon they each get. This measurement gives either left (0) or right (1) outcomes.
   ‍
6. Each of Alice and Bob can then choose to make one of two kinds of interventions x, y ∈ {1, 2}. In the first, (if x=1) then Alice will open the door to Charlie’s lab and ask Charlie what measurement she made. Then Alice will assign Charlie’s outcome to be her own outcome. Alternatively, (if x=2) then Alice will herself measure the laboratory system directly. This measurement can be different than looking at Charlie’s measurement. For example, Alice could decide to weigh the lab to see how heavy it is. When Alice measures the laboratory she is measuring the joint system that includes S_C and Charlie and anything else in the lab. Similarly, if Bob chooses y=1 then he will ask Debbie for her recorded measurement, and if Bob chooses y=2 then he will measure the laboratory system that contains Debbie and S_D.
   ‍

The setup is diagrammed in this Figure from Haddara and Cavalcanti.

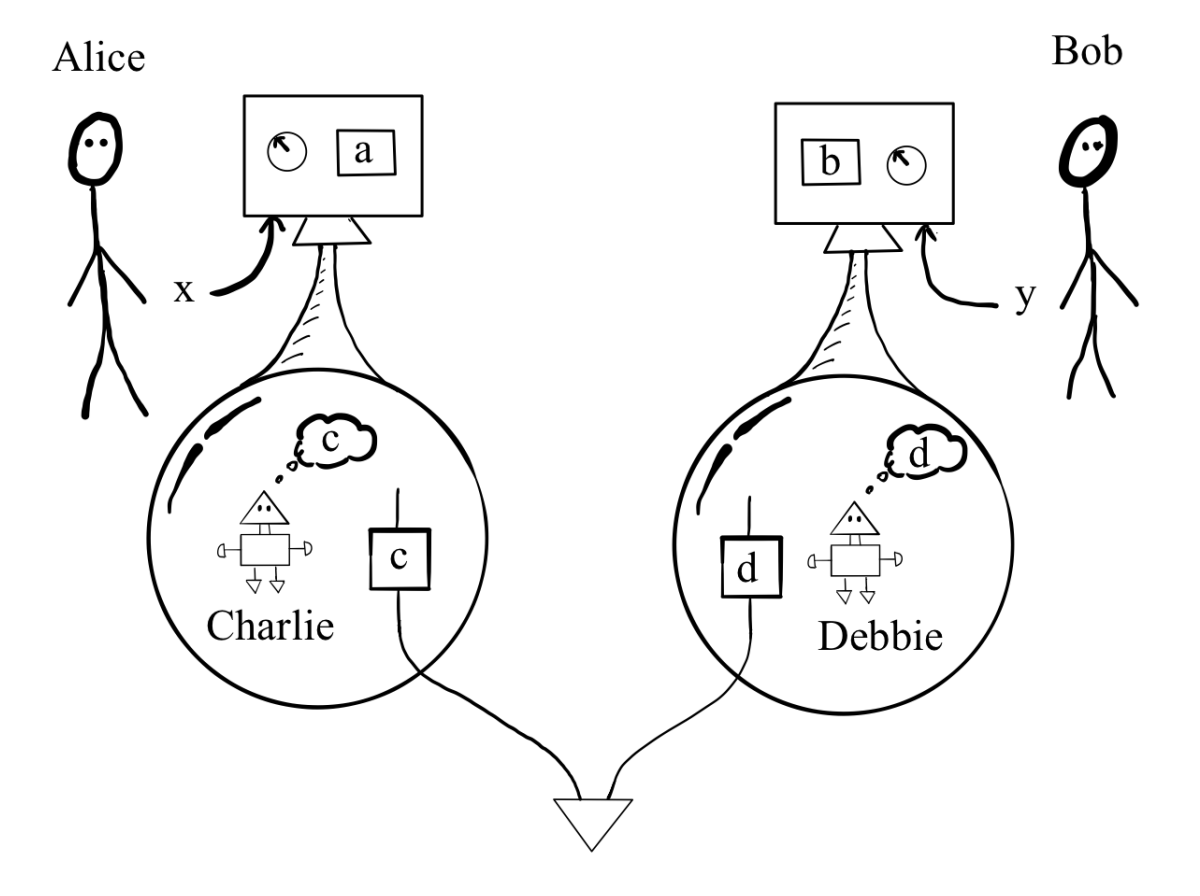
The triangle at the bottom represents the system that is broken into two parts and given to the laboratories containing Charlie and Debbie respectively. Alice and Bob then choose which intervention setting x and y to make. The choice of setting then gives outcomes a and b. The laboratories are separated so that Alice and Bob’s choices of x and y are independent given the PLA assumption.

At the end of the day, we are going to look at the binary observations and choices of interventions that Alice and Bob each make. An event E is given by the quadruple (A, B, X, Y) that describes Alice’s binary observation A, Bob’s binary observation B, Alice’s intervention X, and Bob’s intervention Y. For example, we could observe that the event

E = (A=1, B=0, X=2, Y=2)

is possible. We’d see this if we performed the experiment with both Alice and Bob having chosen to measure the laboratory and Alice having observed outcome 1 while Bob observed outcome 0.

How could this cause a contradiction between AOE and PLA?

Consider an example of potential outcomes that, if they were observed by Alice and Bob, would entail the contradiction. Suppose the event

E₁ = (A=1, B=1, X=2, Y=2)

is possible, while the events

E₂ = (A=0, B=1, X=1, Y=2)
E₃ = (A=1, B=0, X=2, Y=1)
E₄ = (A=1, B=1, X=1, Y=1)

are impossible. Assume all other events are possible. Right now we are just imagining this set of possible and impossible events. We assert this to show that if this combination of possible and impossible events were to be observed then we would have a contradiction. Let’s see how the contradiction plays out.

Applying AOE, the possible events in E₁ occur along with observed values for Charlie and Debbie. That means that the event 

(A=1, B=1, C=c, D=d, X=2, Y=2)

is possible for some values of c and d, while the events from E₂, E₃, and E₄ must be impossible for any values of c and d. 

Now let’s consider what happens if we take a possible event but imagine what would have happened if Alice or Bob had chosen differently. Because of the PLA assumption, we know that Alice’s choice could only affect her outcome and not that of Bob, Charlie or Debbie. Thus, if we have Alice instead choose intervention 1, then the event

(A=a, B=1, C=c, D=d, X=1, Y=2)

should be possible for some value of a. Similarly, we could have Bob change his intervention, which means 

(A=1, B=b, C=c, D=d, X=2, Y=1)

should be possible. Or, having them both change their intervention means that 

(A=a’, B=b’, C=c, D=d, X=1, Y=1)

is possible. Importantly, all of the values of c and d are unchanged in the above examples because Alice and Bob make their intervention choices after Charlie and Debbie observe their outcomes. Due to PLA, Alice and Bob’s intervention choices don’t affect those outcomes.

Recall that in the definition of the experiment, when Alice or Bob chooses intervention 1, they will then set their outcome to the outcome observed by their friend. This means that the following events are possible:

E₅ = (A=c, B=1, C=c, D=d, X=1, Y=2)
E₆ = (A=1, B=d, C=c, D=d, X=2, Y=1)
E₇ = (A=c, B=d, C=c, D=d, X=1, Y=1)

Since E₂ is impossible, it must be the case that in E₅ Charlie’s outcome c = 1. Similarly, because E₃ is impossible, it must be that in E₆ Debbie’s outcome d = 1 as well. This means that c and d should both be 1. However, E₄ means that in E₇ c and d cannot both be 1. This means that there is no consistent value for c and d! Thus our assumptions of AOE and PLA have led to a contradiction.

The bottom line is that there could be results from the Possibilistic Extended Wigner's Friend scenario that shows a contradiction between AOE and PLA. You might be fine with this, by saying that, while the experiment could conceivably give these results, this couldn’t happen in the real world because AOE and PLA are so obviously true. Just wait…

An Aside: This contradiction follows the structure of Hardy’s paradox from 1993. Hardy's paradox has since been generalized in a lot of ways along with other types of ‘All vs. Nothing’ experiments, e.g. Abramsky et al 2017 and some work from Stefano Gogioso and me. One can view the extended Wigner's Friend experiment and contradiction described here as an instance of larger families with different numbers of friends and measurements outcomes and system sizes, etc. The contradiction described here isn't there only one, there are many that quantum mechanics supports.

Does quantum mechanics predict that the experiment will produce contradictory outcomes?

Yes! This should be more than a bit unsettling. It turns out that if quantum mechanics applies in the usual textbook manner then we actually would expect to see the contradiction. We’ll show this using a literate code style to talk you through the few calculations. This part assumes the background of standard quantum mechanics.

We'll start with some basic imports:

import numpy as np

from pyquil.wavefunction import Wavefunction
# We'll use pyQuil's Wavefunction class to pretty print
def pprint(wvf : np.ndarray):
    print(Wavefunction(wvf))

We'll show that quantum mechanics supports this contradiction by giving a specific example of a system state and measurement configurations for Alice, Bob, Charlie, Debbie.

The system will be defined as an even superposition between the |00⟩, |01⟩, and |10⟩ states.

sys = 1/np.sqrt(3) * np.array([1, 1, 1, 0])
pprint(sys)

(0.5773502692+0j)|00> + (0.5773502692+0j)|01> + (0.5773502692+0j)|10>

The measurement settings will be defined by observables in the usual computational and X basis.

zero = np.asarray([1, 0])
one = np.asarray([0, 1])
basis = [zero, one]
_ = [pprint(ee) for ee in basis]

(1+0j)|0>
(1+0j)|1>

# We can define the X basis by applying the Hadamard transform
hadamard = 1/np.sqrt(2) * np.asarray([[1, 1], [1, -1]])
xbasis = [hadamard@ee for ee in basis]
_ = [pprint(ee) for ee in xbasis]

(0.7071067812+0j)|0> + (0.7071067812+0j)|1>
(0.7071067812+0j)|0> + (-0.7071067812+0j)|1>

Now, for each of Alice and Bob, we will define observables that correspond to those bases. Recall from the scenario set up, that is we set x or y to 1 then Alice and Bob will open up their respective friend's laboratories and ask for the result of Charlie's (or Debbie's) computational basis measurement. This corresponds to looking at a computational measurement in the standard basis.

When x or y is instead set to 2, then Alice (or Bob) will make a measurement of their friend's laboratory in the X basis. In practice this could be achieved by doing a Hadamard gate on the joint system of the friend and the part of the system S that they have in their lab.

def observable(x):
    if x == 1:
        return basis
    if x == 2:
        return xbasis

Next we need a few helper functions to implement the standard Born rule from quantum mechanics. The prob function will now tell us the probability of an outcome given by a projector to be obtained from an underlying state.

def dagger(state : np.ndarray) -> np.ndarray:
    return np.conj(np.transpose(state))

def prob(proj, state):
    return dagger(state)@proj@state

We now have enough to calculate the probabilities for different bit outcomes for Alice (a) and Bob (b) under their respective measurement settings x and y.

def experiment(a, b, x, y):
    # measurement projector for Alice
    proj_A = np.outer(observable(x)[a], observable(x)[a])
    # measurement projector for Bob
    proj_B = np.outer(observable(y)[b], observable(y)[b])
    proj = np.kron(proj_A, proj_B)
    return prob(proj, sys)

For example we can look at the probability that Alice and Bob both get a 1 when they have both set their measurement settings to 2. As this is non-zero we would mark this as a possible outcome. Note that this is event E₁ that we need to be possible for a contradiction.

experiment(a=1, b=1, x=2, y=2)

0.08333333333333333

We can now check to see if events E₂, E₃, and E₄ are impossible (have probability 0). If they are impossible then we have all the needed events for the contradiction described in the previous section.

print("E_2 probability is: ", experiment(a=0, b=1, x=1, y=2))
print("E_3 probability is: ", experiment(a=1, b=0, x=2, y=1))
print("E_4 probability is: ", experiment(a=1, b=1, x=1, y=1))

E_2 probability is:  0.0
E_3 probability is:  0.0
E_4 probability is:  0.0

Thus quantum mechanics supports a Possibilistic Extended Wigner's Friend Scenario contradiction between the assumptions of Absoluteness of Observed Events and Possibilistic Local Agency.

Could we actually run this experiment?

Probably not anytime soon if the observers are actually people. While the theoretical setup is simple compared to the many operations in quantum algorithms, there are some significant challenges in trying to build the experiment that is described above. First off, if Charlie and Debbie are people, then you need to put them in superposition and Hadamard them!

Over the last century, we've gotten a lot better at controlling larger and larger quantum systems but there are reasons to believe that this could be very hard [6] [7] if the observers really are people.

However, it isn't clear that only people count as observers of events. What is it about people that makes them a special kind of system that can observe? Is it that observers have many degrees of freedom, large mass, are irreversible in some sense, have consciousness or agency? All of these characteristics are the type of dimensions that have variously been argued to be important for observerness. 

One could imagine a research  program that experimentally tests the Possibilistic Extended Wigner's Friend Scenario with Charlies and Debbies of increasing size and sophistication. Everyone agrees on the outcome of the experiment when the “observers” are small, controllable quantum systems and experiments have already been successful at the smallest of these scales.

However, since these systems are small, one could be comfortable with denying them an observed reality. As we scale them up, this denial becomes more tenuous. For example you might get to scales where the systems have “thoughtfulness” that should give them observer status, as argued in this recent work by Wiseman, Cavalcanti, and Rieffel. This is analogous to the program of building larger and larger fault tolerant quantum computers, but with a different technical goal. Alternatively, you could see this like the pursuit of particle physicists to confirm the standard model by working at bigger and greater energy scales. We'd be confirming, or breaking, deep implications of quantum mechanics at larger and larger scales.

There are many open questions about what such a program could look like, even at the beginning. And one would need to be careful, for example, not to start a moon landing program where we are building higher and higher ladders. Focusing on eventual scalability is important.

Still, the metaphysical questions raised by this thought experiment are enormous and deserve a serious program of research. Especially when that research is hard and sits at the boundary of philosophy and physics.

I know I'll be thinking about this more. If any of this intrigues you, then subscribe below for updates or reach out to me at will@unitary.fund.

Acknowledgements

With thanks to Ankur Desai, Marcos Carzolio, Bary Pradelski, Milan Cvitkovic, and Dan Girshovich for reviewing this article and to Caslav Brukner, Eric Cavalcanti, and Howard Wiseman for pointing out to me how important these experiments could be and for stimulating discussions besides.